Rosetta Energy Function
Overview
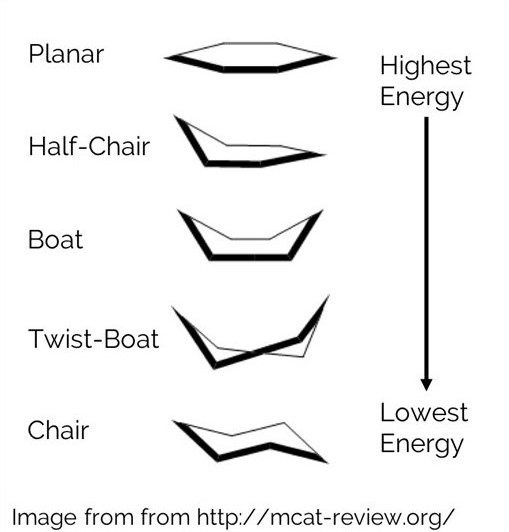
An Energy Function is one of the most important tools for modeling a molecular structure. It provides a way to determine if a structure is favorable compared to alternate conformations of the structure. For example, a hexose molecule molecule can form the 5 conformations shown below. Each one can be scored in order to determine which is most likely to occur. Since the chair conformation has the best energy, it is the most favorable.
We use the Rosetta full atom Talaris2013 energy function to score protein conformations in Bench in order to determine which conformation is the most favorable. This combines energy terms that are both physics-based and statistics-based. The physics terms take into account the bond lengths/angles, proximity and types of atoms present, and sums up the physical forces for all atoms present. The statistical terms take into account the propensity of structural features found in nature. Statistical terms were gathered from structures found in the PDB and from other experimentally derived knowledge of molecular structures. The physical and statistical potentials are summed and reported on an arbitrary scale referred to as Rosetta Energy Units (REUs).
The energy score of your protein structure is not a measure of whether the structure can truly exist in vivo. It is a relative term that is not comparable across different structures that lack similarity. It is generally accepted that lower energy translates to a more favorable conformation than higher energy. While REUs cannot be directly converted into kcal/mol free energy, when calculating ΔΔGs of point mutations there is a strong correlation (up to 0.73) with experimentally determined kcal/mol (Kellogg et al).
In order to put a structure’s energy into a functional context, many people describe the relationship between a molecule’s energy and its structural conformation using an energy landscape. An energy landscape is a hypothetical map of all possible conformations of your structure graphed in terms of energy.
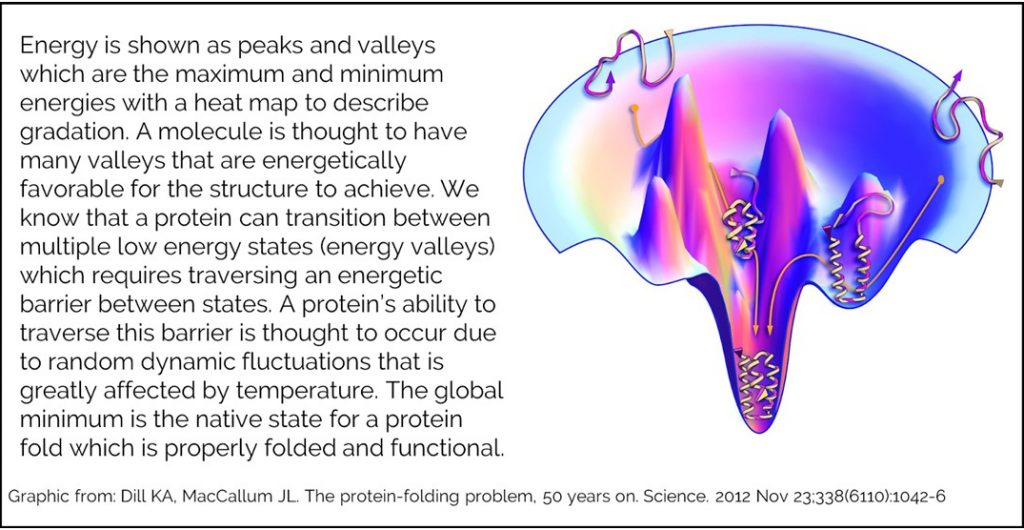
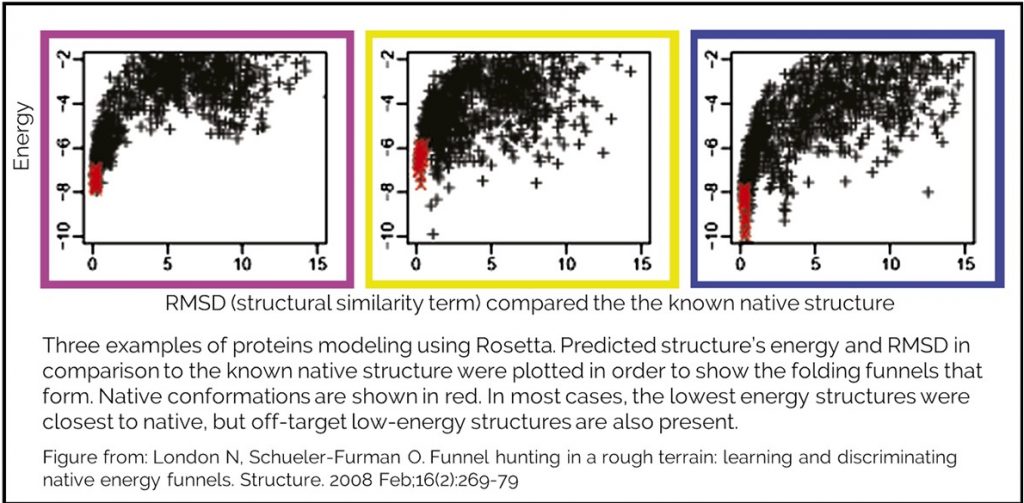
Our energy function cannot tell you whether you have reached the native state, but can guide you towards it. Testing has been done to measure how well our energy function does when attempting to model a native state. Creating a good model requires an accurate energy function and a robust method for sampling conformations. Rosetta labs have modeled many protein structures in attempt to recapitulate known native structure. During this process, they generate hundreds or thousands of structure that they rank by REU.They have shown that successful modeling will generate an energy funnel. The lowest energy structures are the most similar to the known native.
What are the components of the Rosetta Energy Function?
When Rosetta calculates the an energy score for a molecule’s conformation, it is actually calculating 12 different kinds of energy terms.
- Lennard-Jones Attraction and Repulsion Forces between different residues
- Lennard-Jones Repulsion Force between atoms of the same residue
- Coulombic Electrostatic Potential
- Lazaridis-Karplus Solvation Energy
- Proline Closure Term
- Hydrogen Bond Energy
- Disulfide Geometry Potential
- Ramachandran Preferences
- Harmonic Constraint for Backbone Omega Dihedral Angles
- Side Chain Rotamer Term using Dunbrack’s 2010 Statistical Library
- Probability Term of an Amino Acid given a Phi/Psi angle
- Reference Energy for each Amino Acid – Average energy of each amino acid in the unfolded state
These 12 terms fall into 5 different categories explained below.
Lennard Jones (LJ)
This is a physic-based energy term. It is the measure of the energy for two atoms that is dependant on the distance between the atoms. There is an equilibrium distance between two atoms that has the lowest possible energy, aka the energy well. As atoms become closer than that ideal distance, the energy dramatically rises. As they become further apart. The energy slowly rises until it asymptotically becomes zero.
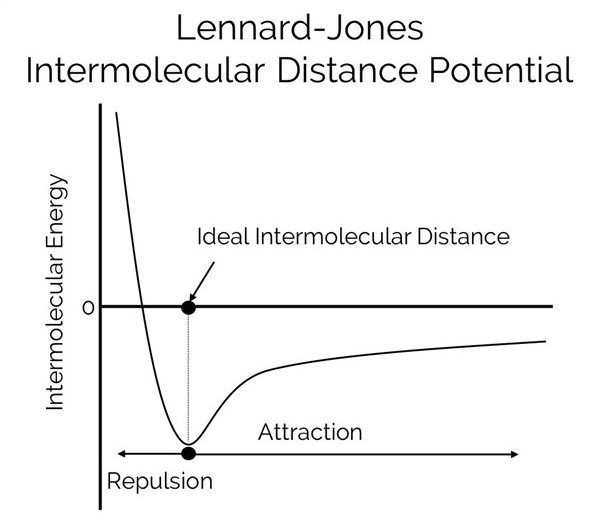
The LJ score is calculated as a sum of attractive and repulsive forces.
The repulsive component measures the short range repulsion which is also called Pauli Repulsion. The repulsion is driven by interaction of electron orbitals. This is often called a steric clash.
LJ Repulsion = (Distance when energy is zero / Actual distance) [12]
The attractive component measures the long range attraction which includes Van der Waals and Dispersion Force. Van der Waals describes the weak force that pulls atoms together Dispersion Force is attraction due to transient dipole attraction.
LJ Attraction = (Distance when energy is zero / Actual distance) [6]
Total LJ = (Depth of energy well) x ( (LJ Repulsion) – 2(LJ Attraction) )
Backbone Torsion
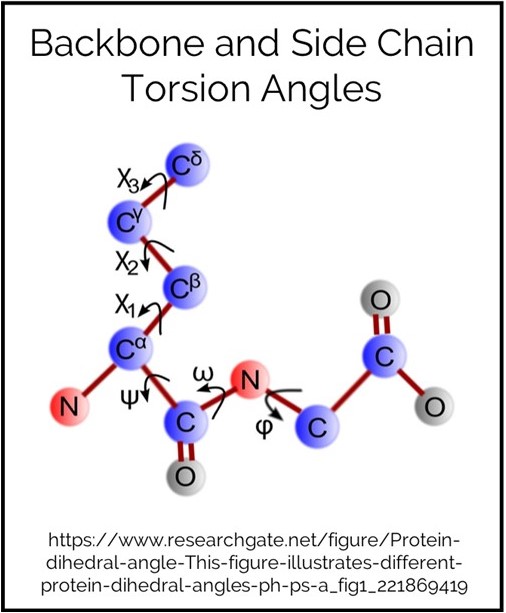
This is a statistic-based energy term. Torsion angle refers to the covalent bonds in the protein (excluding bonds with hydrogens). The backbone has three angles per amino acid which are called φ (phi), ψ (psi) and ω (omega) bonds.
Side Chain Torsion
The number of torsion angle bonds in a side chain is, of course, dependant on the size of the side chain. Glycine’s side chain is only a hydrogen so does not have any torsion angles. The C alpha is part of the backbone, so the first torsion angles refers the angle between this and the C beta. Subsequent bonds are named sequential with the greek alphabet.
Hydrogen Bonds
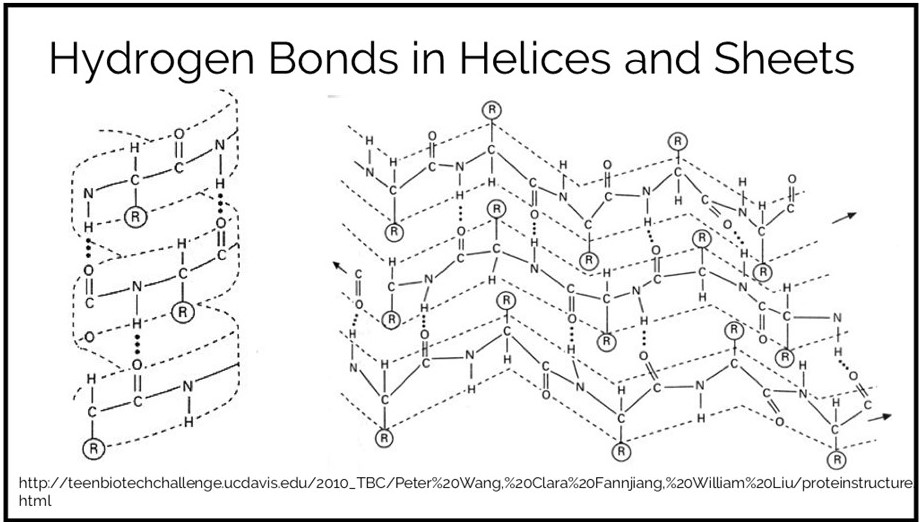
This is another physics-based score term. It measures the energy of noncovalent interactions that include a hydrogen. This is a partially electrostatic interaction. Since hydrogens that are a part of a covalent bond are slightly positive, they will be attracted to slightly negative atoms such as nitrogen and oxygen. While individual hydrogen bonds are relatively weak, there are a great number of hydrogen bonds in a folded protein, so this term can be a strong driving force behind protein stability. They are responsible for maintaining many kinds of protein motifs including alpha helices and beta sheets.
Solvation
Rosetta does not include water molecules during modeling, so it has an implicit solvent included in scoring. This is called the Lazaridis-Karplus (LK) score and is a physics-based term. There is a penalty for buried polar groups and a favorable score is given to buried nonpolar groups.
How is the Rosetta Energy Function optimized?
Many research labs in the Rosetta community have done significant testing to optimize this energy function. This is done with benchmark sets, which are sets of structures with experimental data. Each set represents common modeling approaches for Rosetta including; recovering of native sequence starting from a known fold, recovering of native rotamers for a given backbone, discrimination between non-native modeled structures vs native, predicting ddG of point mutations, predicting loss of function.
There are several variations that are optimized for specific modeling cases, but the default energy function was designed to be broadly useful for diverse modeling tasks. Variation is controlled by giving a weight to each energy term. Weights are benchmarked, meaning they are testing to see what weights correlate with experimental data. With that in mind, the energy function used by Cyrus was sharpened by testing weights on the energy terms against several benchmark types in order to find a balance that is the most predictive for varied testing sets.
Individual features such as characteristics of hydrogen bonds or bond geometry were analyzed separately to see how parameterization of energy terms affected these features. For example, increasing the weighting for the hydrogen bond term could lead to a more accurate score for protein interactions, but make it less accurate for small molecule docking. All potential applications of Rosetta are considered in order to find the balance of weights that is most predictive across the board.
For a more detailed understanding of energy functions, we recommend these references…
London N, Schueler-Furman O. Funnel hunting in a rough terrain: learning and discriminating native energy funnels. Structure. 2008 Feb;16(2):269-79
Kellogg EH, Leaver-Fay A, Baker D. Role of conformational sampling in computing mutation-induced changes in protein structure and stability. Proteins. 2011 Mar;79(3):830-8
Dill KA, MacCallum JL. The protein-folding problem, 50 years on. Science. 2012 Nov 23;338(6110):1042-6
Leaver-Fay A, O’Meara MJ, Tyka M, Jacak R, Song Y, Kellogg EH, Thompson J, Davis IW, Pache RA, Lyskov S, Gray JJ, Kortemme T, Richardson JS, Havranek JJ, Snoeyink J, Baker D, Kuhlman B. Scientific benchmarks for guiding macromolecular energy function improvement. Methods Enzymol. 2013;523:109-43
Alford RF, Leaver-Fay A, Jeliazkov JR, O’Meara MJ, DiMaio FP, Park H, Shapovalov MV, Renfrew PD, Mulligan VK, Kappel K, Labonte JW, Pacella MS, Bonneau R, Bradley P, Dunbrack RL Jr, Das R, Baker D, Kuhlman B, Kortemme T, Gray JJ. The Rosetta All-Atom Energy Function for Macromolecular Modeling and Design. J Chem Theory Comput. 2017 Jun 13;13(6):3031-3048.